Directed HyperLMNtal
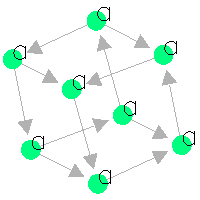
This is an experimental project
Directed HyperLMNtal (DHLMNtal) is a derived calculus model of LMNtal. It is designed to be able to deal with hypergraphs representing structures and pointers easily without having dangling pointers.
Installization
- Requirement
- stack (haskell).
git clone https://github.com/sano-jin/vertex.git
cd vertex
stack build
Introduction
Atoms and Links
DHLMNtal program is consists of graphs. Graphs are consists of Atoms (= nodes) and Links (= directed hyper edges).
- Links
- links are denoted by identifiers starting from capital letters.
- When representing a graph, links must appear inside of the link creation
\X1 X2 ... Xn.<inside the link creation>. - E.g.
X,Y, …
- Atoms
- An atom has an incomming link, its name and 0 or more outgoing links.
Denote them as
<the incomming link> "->" <the name of the atom> "(" <the outgoing links> ")".- The name can be an identifier starting from small lettes.
- You can omit the parentheses if there is no outging link and
- you can omit the incomming link if the link doesn’t appear other than it.
- E.g.
X -> a(Y, Z),X -> b,c, …
- An atom has an incomming link, its name and 0 or more outgoing links.
Denote them as
Separate atoms with commas.
For example, you may write like this.
\X.(a(X), X -> b)
Open your favorite editor, write down the former program, save it as test1.dhl and visualize it with the dhlvis.
stack exec dhlvis -- test1.dhl
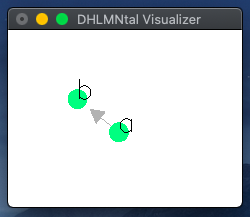
Press ESC to terminate.
There also are several abbreveation schemes for convenience.
For example, a(b) is as same as the former \X.(a(X), X -> b).
Since you can embed the atom where the outgoing link should occur
and omit the link creation if the outgoing link and the incomming link of the atom are the same
and there is no other occurrence in the link creation.
Rules
Besides the graphs, you can write the (rewriting) rules <left hand side: subgraph to match> ":-" <right hand-side: subgraph to yield>.
The rule will rewrite the graph to its right hand-side if it’s left hand-side mathces.
Notice the rule remains and tries to rewrite graphs until it fails.
You can use period to separate graphs and rules.
Rewrite the former program as the following
a(b).
X -> b :- X -> c.
and visualize it.
stack exec dhlvis -- test1.dhl
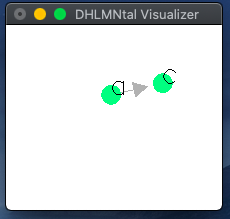
Press SPACE to reduce (rewrite) 1 step.
If you want the reduction steps in a text, run dhli.
stack exec dhlvis -- test1.dhl
The output will be the following.
0:
a(b).
1: X -> b :- X -> c ~>
a(c).
This shows
- The initial state is the
a(b)(and the rule), - the reduction
~>proceeds with a ruleX -> a :- X -> cand - the second and the terminal state is
a(c)(and the rule).
Notice that the rule is hided for the simplicity but it does exist throughout the calculation process.
Non-detereminisity
DHLMNtal has non-detereminisity. Rules can rewrite graph as long as they matches, they are not ordered.
For example, the resulting graph of a. a :- b. a :- c can be b or c.
You can use --nd (non-deterministic) option to construct the state transition space (all possible states and reduction).
This can be also applied to the not-terminating program.
For example, example/nd/cycle.dhl is a following program.
a.
a :- b.
b :- c.
c :- d.
d :- e.
e :- f.
f :- a.
You can run this with the --nd option.
stack exec dhli -- example/nd/cycle.dhl --nd
Also, you can visualize the state transition space.
Run stateViewer as below.
stack exec stateViewer -- example/nd/cycle.dhl
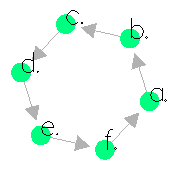
You can easily see that the transitions are forming a cycle and there is no terminal state.
For more informations
See here to get more description about semantics. This pdf also describes the semantics.
Also, feel free to take a look at the slide (its written in Japanese though).
Tools in a nutshell
dhli- the ordinary (one-way) execution if you put no option.
- E.g.
stack exec dhli -- example/sample.dhl
- E.g.
- put
--ndfor the non-deterministic execution- E.g.
stack exec dhli -- example/nd/cycle.dhl --nd - add
--show-allfor more detailed result (this shows the all transitions).
- E.g.
- the ordinary (one-way) execution if you put no option.
dhlvis- visualizes the graph rewriting process in the ordinary execution.
- E.g.
stack exec dhlvis -- example/vis/cube.dhl
- E.g.
- visualizes the graph rewriting process in the ordinary execution.
stateViewer- visualizes the state transition space (all possible states and the transitions).
- E.g.
stack exec stateViewer -- example/nd/cycle.dhl
- E.g.
- visualizes the state transition space (all possible states and the transitions).
Development
Test
Run this test to obtain more detailed information about the state of the heap, etc.
stack test --test-arguments "example/sample.dhl"
Also, see here to get more information about testing this.