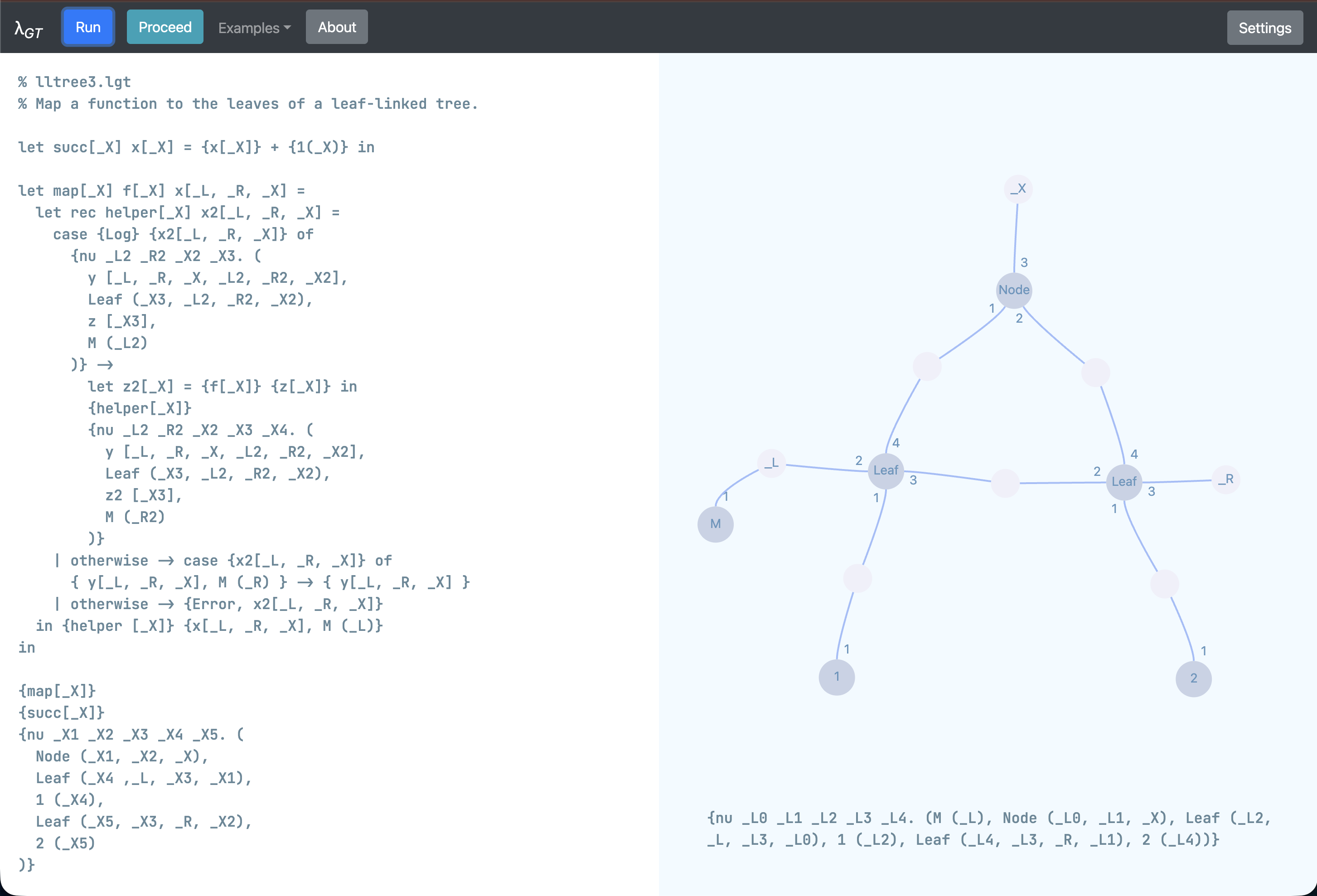
私の研究テーマの紹介をしたい.
私は(休日は),プログラミング言語の研究と称して, $\lambda_{GT}$ と名付けたプログラミング言語をつくっている.
プログラミング言語の研究はもちろん山程あるが, 私の研究のどこが新しいのかというと, 「(ちょっと)複雑なデータ構造も宣言的に型安全に扱える」 ということ.
これだけだと抽象的すぎるので,具体例で説明したい.
まずは,「普通の・既存の言語ではデータ構造をどう扱うか?」について考えてみる.
普通の・既存の言語ではデータ構造をどう扱うか?
まずは一番簡単なデータ構造の例として,「リスト」について考える.
まずはどう定義するかを見ていく.
データ構造の型定義
C/C++ や Java などの命令型言語 (Java はオブジェクト指向だが,今考えている範疇だと命令型言語と思って良いはず)では, こんな感じにノードを定義することになる.
/* Define the node structure */
typedef struct Node {
int data; /* リストの要素 */
struct Node *next; /* 次のノードへのポインタ */
} Node;
OCaml や Haskell などの関数型言語だと, もっと綺麗に定義ができる.
※ そもそも何をもって「関数型言語」と呼ぶかがかなりややこしいが, ここでは OCaml や Haskell などの,
- 静的型付きで,
- 関数を関数の入出力として扱えて(そしてそれが普通で),
- パターンマッチングとかがある
言語のことを指すことにしたい. つまり,Lisp とかではない.
例えば
type list = Nil | Cons of int * list
はリストを定義している.
これは,
リスト list は
- 「空のリスト(
Nil)」か - 「要素(整数)と後続のリストの組(
int * list)」
のどちらかだと言うことを示している.
データ構造の操作
C/C++ や Java などの命令型言語ではポインタ・参照を駆使してデータ構造を扱うことになる.
例えばリストの要素を全て + 1 したいときは,こんな感じになる.
/* 各要素を +1 */
void increment_list(Node *head) {
while (head != NULL) {
head->data += 1;
head = head->next;
}
}
これくらい単純なプログラムであればバグらせようもないかも知れないが, 一般にポインタを扱うプログラムは非常にバグらせやすい.
特に C/C++ では容易に未定義動作を引き起こす.
関数型言語ではこのようなデータ構造の操作を「パターンマッチング」で宣言的に記述することができる.
例えばリストの要素を全て + 1 したいときは,
let rec f xs = match xs with
Nil -> Nil
| Cons (y, ys) -> Cons (y + 1, f ys)
(* y は要素, ys は後続のリスト *)
のように書ける.
そもそもリストは
- 「空のリスト(
Nil)」か - 「要素(整数)と後続のリストの組(
int * list)」
であると定義したので, それに従ってパターンマッチングで分解しているだけ.
わかりやすい.
ここでは,これを「宣言的に書ける」と言うことにする.
※ 関数型言語では map 関数を使ってもっと簡単に書ける.今回の例は
let f = map succ (* succ は Pervasives に定義されている関数 (fun x -> x + 1). *)だけで書ける.
ただここではデータ構造を直接操作するプログラムについて考えたいので, そのような例になっている.
map 関数を使う前提だとしても, map 関数自体は上記のようにパターンマッチングを使って書かれており, ここでの議論が同様に成り立つ.
関数型言語では, 定義に沿ってパターンマッチングで分解して, 分解して得られるものに対して網羅的に操作を定義しているので, 変なところで変なこと(未定義動作を引き起こしたりなど)を起こさないということが保証できる.
関数型言語は, 型定義も綺麗だし, 実際の操作も宣言的に書けるし, 型安全だし, 非常にプログラミングしやすい.
実際,Rust などの比較的新しい言語は,こうしたいわゆる関数型言語の特徴をどんどん取り込んでいる.
問題
関数型言語では, リストやツリーなどのシンプルなデータ構造であれば, 綺麗に型定義して宣言的かつ型安全に操作ができる.
ただし,一般に「データ構造」と言ったときに, 素朴なリストやツリーだけしかないかと言われると,そうではない.
例えば 双方向連結リスト とか,手続き型言語ではかなりよく使われる.
他にも スキップリスト や
葉が接続されたツリー など,
色んなデータ構造があり得る.
残念ながら,既存のプログラミング言語ではそもそもこういうデータ構造の型を定義することからできない.
例えば, 双方向連結リストを構成する「ノードの型」とか, 双方向連結リストの「操作のインタフェース」を定義することはできるが. そもそもの「双方向連結リストの形状をちゃんと定義する」ことが,できない.
例えば C/C++ で以下のように双方向連結リストの「ノードの型」を定義したとする.
/* Define the node structure */
typedef struct Node {
int data; /* リストの要素 */
struct Node *prev; /* 前のノードへのポインタ */
struct Node *next; /* 次のノードへのポインタ */
} Node;
これは正しい定義ではあるのだが, 「この型定義に従うものが双方向連結リストに必ずなる」という保証はない.
例えば,以下の図のように,
「prev が一つ前のノードではなく,自分自身を参照してしまっている」
などのバグがあっても既存の型チェックでは発見できない.
上記のようになっていると,
「prev を辿って先頭の要素まで逆順に取得していこうとした際に無限ループする」
などの,
厄介なバグを引き起こす.
残念ながらポインタ・参照を操作していると, こういうバグは頻出する.
関数型言語では (raw) ポインタではなく, 「参照」を用いて上記のようなデータ構造を定義し, 操作することになるのだが, いずれにせよ同様の問題が発生する.
個人的には,このように,
- リッチなデータ構造の操作は煩雑で誤りやすい.
- なのにそれらの操作が正しいか(変なデータ構造になっていたりしないか)の型チェックはできない.
というのは残念な状況であり,解決されるべき課題だと考えている.
目標
私がやりたいのは, 「(ちょっと)複雑なデータ構造も宣言的に型安全に扱える」 ということ.
- 例えば双方向連結リストやスキップリスト,葉が繋がったツリーなどの, 素朴なリストやツリーではないようなデータ構造であっても,
- 既存の関数型言語が素朴なリストやツリーを扱うように,
- ユーザが簡単に帰納的に型定義して,パターンマッチングによる宣言的な操作ができるようにしたい.
そのようなプログラミング言語の実現を目標としている.
補足)
- 一般的な研究の方向性としては, 「既存の手続き型言語の拡張として, (高度な)検証系を導入する」というのが良くある気がする.
- 今回はそもそも新しい言語を作ってしまおうとしており, かなり方向性が違う1.
補足) これは単なる私の感想だけども, Gemini/ChatGPT/Qwen/DeepSeek などのいわゆる AI ($\supseteq$ LLM) がさらに発展しても, ソフトウェア検証($\supset$ 型システム)は重要な技術として残ると思う.
- LLM は(少なくとも現状は)統計的処理に基づいており,一定以上の確率で「間違える」のは変わらないはず.
- むしろいわゆる AI にプログラミングを任せる割合が増えると, 下手にブラックボックス化して, より困ったことになる可能性すらあると思う. この先無限に性能向上した際にどうなるのかは正直よく分からないが, 少なくとも今はそういう感じがある.
- 特にデータ構造の操作ミスは,メモリ不正などの見つかりづらく・重大なバグを引き起こす可能性がある.
アプローチ
上記目標を達成するためにとれるアプローチは色々あるかもしれないが, 私のとったアプローチは以下の通りになる.
- まず上記データ構造を全て包含する「(ポートハイパー)グラフ」 をパターンマッチングで宣言的に操作できる言語を設計した.
- そしてその言語のためのデータ構造を帰納的に型定義可能な型システムを設計した.
これが表題にもある $\lambda_{GT}$ (Lambda GT) である.
Lambda + GT は,Lambda Calculus (関数型言語のコア理論) と Graph Transformation (グラフのパターンマッチングと書き換え) に由来している.
$\lambda_{GT}$ の動作例
$\lambda_{GT}$ では,例えばこのようなデータ構造を扱うことができる.
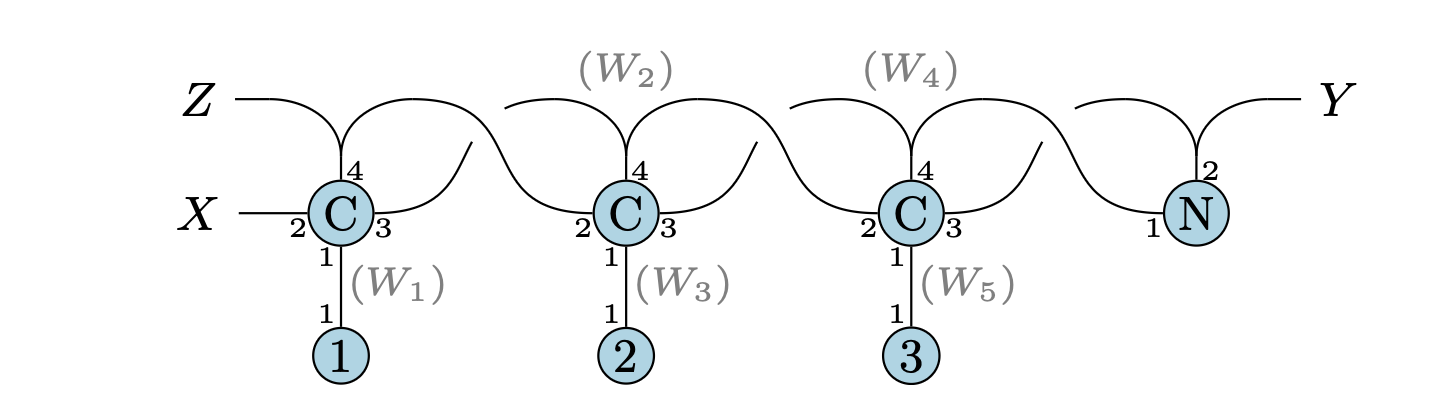
図において,C は Cons, N は Nil を意図している.
C/N の周りに書いてある数字は「ポート番号」であり,
直感的には「リンク(辺)」が C/N の何番目の引数になっているかを表している.
リンクを,最終引数になっている部分を矢印の頭 (→) にした「ポインタ」だと思えば, これはまさに C/C++ で扱うような双方向連結リストを表していると思ってもらえるのではないかと思う.
X/Y/Z は外部から参照できるリンクで,
Zはリストの先頭を,Yはリストの末尾を参照している.Xは一つ前の要素を指すポインタが宙に浮いている感じで, この例では不要に見えるが, これは帰納的定義の際に必要になる. C/C++ でリストなどを扱う際に用意する「番兵」みたいなものだと思って欲しい.
W1/W2/W3/W4/W5 は内部に隠蔽されているリンクで,
外部からのアクセスはできない.
上記のようなデータ構造は以下のような帰納的定義によって厳密に型定義できる.
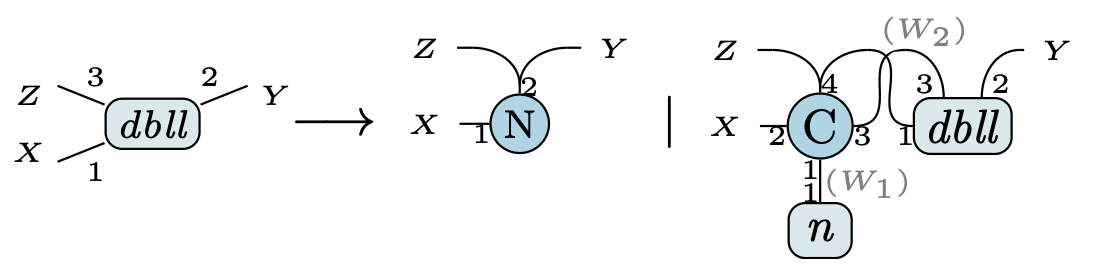
これは,双方向連結リスト dbll は
- 「空のリスト(
Nil)」か - 「要素(自然数
n)と後続の双方向連結リストdbllをうまくリンクで接続したもの」
であることを表している.
これは,普通の関数型言語でのリスト list の定義の自然な拡張になっているのではないかと思う.
(* 再掲 *)
type list = Nil | Cons of int * list
(*
リスト `list` は
- 「空のリスト(`Nil`)」か
- 「要素(整数)と後続のリストの組(`int * list`)」
のどちらか.
*)
上記の方向連結リストの型定義は, 双方向連結リストの「形状」を厳密に定めているので, 「リスト途中でポインタがこんがらがってしまい自己ループしてしまった」などの, 「変なことになっているデータ構造」には型がつかない.
私の知る限り,そもそもこのようにデータ構造の「形状」をユーザが型定義できる言語は, $\lambda_{GT}$ だけである.
※ とは言っても関連研究はもちろん色々ある. 一応知る限りのことを この論文の Section 6 に詳しくまとめたつもりでいる.
このようなデータ構造へのパターンマッチングを行うプログラムは, 例えば以下のように記述できる.
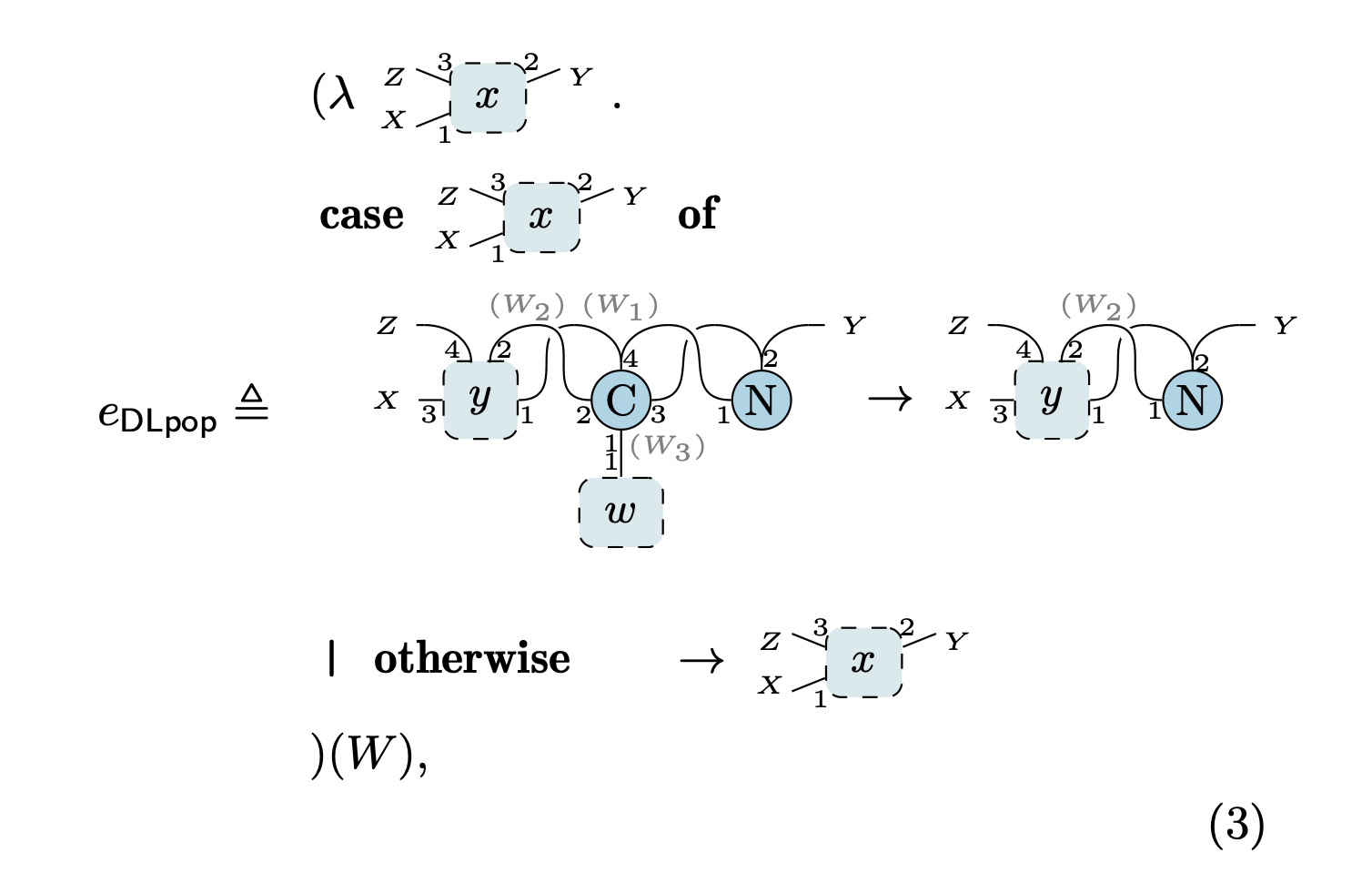
これは双方向連結リストの末尾にパターンマッチして, 末尾の要素が存在すればそれを取り外すという例になっている.
$e_\mathsf{DLpop}$ は $\lambda$ 抽象(関数)であり,
- 1 行目で双方向連結リスト
xを入力として受け取る. - 2 行目以降の case
xof … でこの双方向連結リストxへのパターンマッチングを試みる. - 3 行目は「双方向連結リストの末尾に
Cがある」というパターンになっており, これにパターンマッチできた場合は末尾のCを取り除く. - もしも末尾に
Cがそもそも存在しない場合は, 4 行目で入力として受け取った双方向連結リストxをそのまま返す.
これは末尾の要素を消去する例だが, 例えば末尾の要素を取得するプログラムなどもすぐに同様に書ける.
補足)
- 普通の関数型言語では,リストの末尾の要素へのアクセスはすぐにはできないのに対し, $\lambda_{GT}$ では一回のパターンマッチングでそれが実現できている.
- 特に双方向連結リストでは, 末尾への参照をうまく用いれば, このようなパターンマッチングを $\mathcal{O}(1)$ で実現できるはずで, そのような最適化がなされる処理系が実装できるはずだと考えている. まだ実装できていないが…
- Context Patterns などの通常の関数型言語よりも強力なパターンマッチングが可能な枠組みは研究として存在しているが, リンク(参照)をうまく使うことで,それらよりも効率の良い実装ができると考えている.
上記プログラムは以下のように動作する.
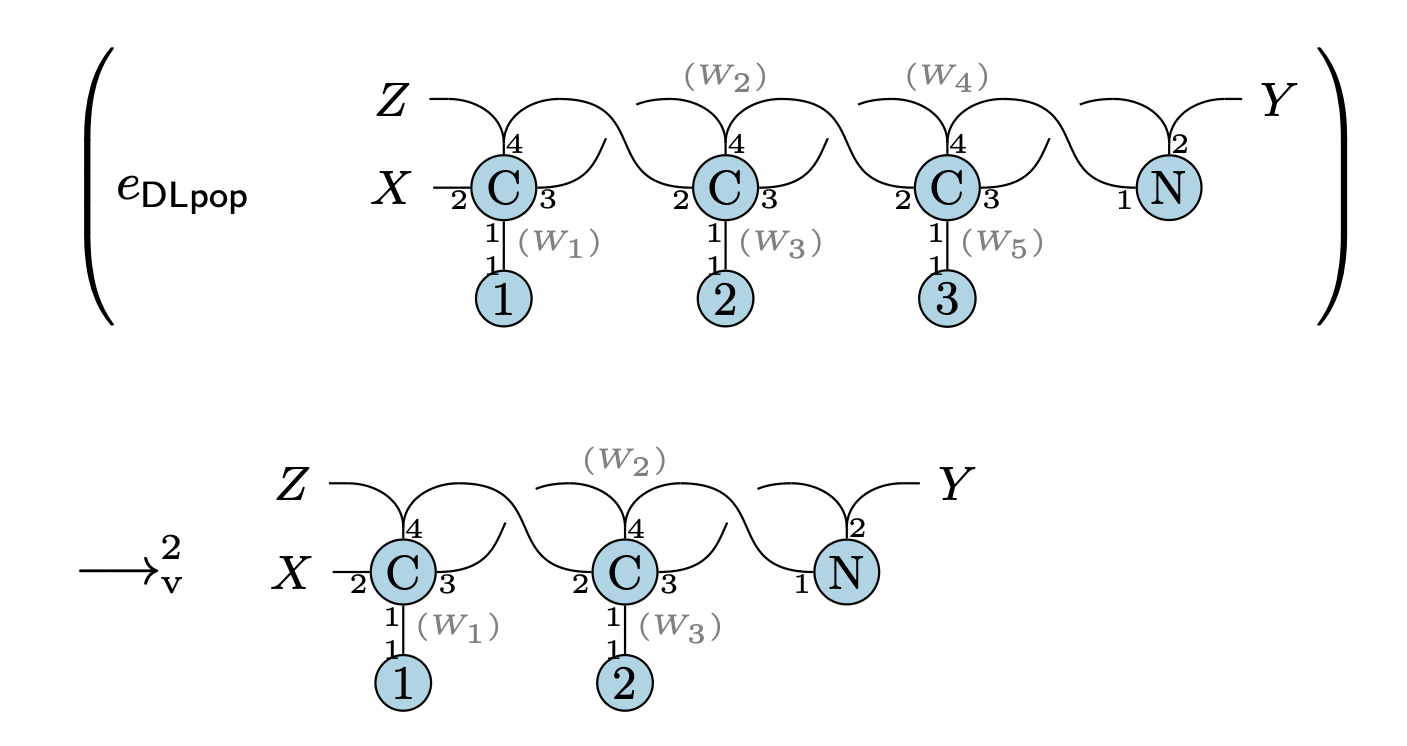
双方向連結リスト [1, 2, 3] に,
先ほど定義した関数 $e_\mathsf{DLpop}$ を適用させると,
末尾の要素 3 がなくなった双方向連結リスト [1, 2] が返ってくる.
研究としてどういうことをしている・いたか
そもそも上記のようなことをするための理論が存在しなかったので, まずは上記のような言語のための理論的枠組みを考える必要があった.
上記では図で説明したが, プログラムの安全性などを数学的に議論するためには, 当然数学的な(テキストベースでの)プログラミング言語の定義が必要になる.
- というわけで,まずは構文と意味論(プログラムの動作の定義)から考えた.
- 一般的なプログラミング言語の研究では, 構文・意味論レベルで新しい言語を設計することはそんなにないのではないかと思う. 型システムとか高度な検証とかの方にかなり寄っている印象がある. 異論は認める. 自分の知識不足は常々感じているし,もしかするとそんなことはないのかもしれない.
- 今回に関しては,正直,これがそもそもそんなに自明ではなかった(気がする). もっとうまくやれたかもしれないというものも色々あるが.
構文と意味論(プログラムの動作の定義)を考えた後は, 型システムを考えて,その型システムの 「健全性(型がついたプログラムは絶対に変なことにならないという定理)」 を証明する.
- ここもかなり手戻りがあった.
- そもそも型システムの設計がダメで,健全性を満たさなかったり, 自分の証明に誤りがあったり…
- 最終的にはコア部分は Isabelle (定理証明支援系)で形式化することにした.
とはいえ正直に言って,良くも悪くもそんなにレベルの高い研究ではないとは思う.
- 数学的に高度なことはしていない. 場合分けしながら帰納法を回しているだけ.
- プログラミング言語理論分野においても, 良くも悪くもかなり初歩的な研究なのではと思う.
- 数学的知識とかがなくとも読める論文しか書いてない.
Preprint だが,こんな感じのことをしている.
あとなにをするか
残念ながら $\lambda_{GT}$ はコア部分の理論がようやくなんとかそれっぽくなりつつある, というくらいの状態で, まだ普通にプログラミングができるような状態にはない.
一応,簡易的なインタプリタは実装した.
- ソースコードを GitHub で公開している.
- たったの 500 行 で実装されている.
- どういう実装かとかはこの論文に書いてあるので, 興味があればぜひ見て欲しい.
ブラウザでも動かせるようにしてある.
ただ,これはあくまで PoC であって,実用に耐えうるような処理系ではない.
あと,型検査器の実装もまだできていない.
将来課題としては,
- 型検査器の実装.
- ただし,これも色々な段階がある.
- 今のところは単純型の素朴な拡張しか考えていないが, polymorphism や type inference, パターンマッチングの completeness に関してなど, 実用言語に向けては色々な課題がある.
- コンパイラ(あるいはトランスパイラ)の開発.
- グラフのパターンマッチングは一般に計算量的に難しい問題だが, 型付けの際の情報を用いるなどすれば効率の良い実装が可能だと考えている.
- 理想的には手続き型言語でポインタを直接操作するようなプログラムと同等の性能 (つまり普通に手続き型言語でポインタを用いて書くようなコードにトランスパイルできるようにする) を目指したい.
- が,たぶん簡単ではない.
などがあり, これらをクリアしないと, 実用化できないが, まぁなんとも難しい.
あとはそもそも現状はあんまり書きやすい構文じゃないというのもある.
以下の双方向連結リストは

理論的には以下のような構文で表すのだが,
\[\begin{array}{lll} \nu W_1 W_2 W_3 W_4 W_5.( \\ \quad \mathrm{Cons}(W_1,X,W_2,Z), 1(W_1), \\ \quad \mathrm{Cons}(W_3,Z,W_4,W_2), 2(W_3), \\ \quad \mathrm{Cons}(W_5,W_2,Y,W_4), 3(W_5), \\ \quad \mathrm{Nil}(W_4, Y) \\ ) \end{array}\]これが読みやすいかと言われると, まぁなんとも言い難いかなと.
研究というよりかは割と表面的な話かもしれないが, 良い感じの糖衣構文を考えたり, あるいはビジュアライザを作ってみたり(?), 色々できること・やるべきことはあると思われる.
一方でフルタイムでの仕事も最近は忙しくなりつつあるので, ちょっと難しさは感じている.
まとめ
休日返上で 「(ちょっと)複雑なデータ構造も宣言的に型安全に扱える」 ことを目指したプログラミング言語の設計をしている.
たまに気が大きくなったときは (相手を選んで) 「Rust を超える世界最強のプログラミング言語を作っている2」 などと宣っているが, 実際のところはまぁこんな感じのことをしている.
共著者や査読者の方にはいつも有用なアドバイスをいただき, 文字通り大変お世話になっている. 感謝申し上げたい.
文献リスト
- Sano, J., Yamamoto, N., Ueda, K.:
Type Checking Data Structures More Complex than Trees.
J. Inf. Process. 31, 112–130 (2023).
https://doi.org/10.2197/ipsjjip.31.112
- $\lambda_{GT}$ の初出.
- Sano, J., Ueda, K.:
Implementing the $\lambda_{GT}$ Language: A Functional Language with Graphs as First-Class Data.
In: Fern{'a}ndez, M., Poskitt, C.M. (eds.) Graph Transformation. ICGT 2023.
Lecture Notes in Computer Science, vol. 13961, pp. 263–277. Springer, Cham (2023).
https://doi.org/10.1007/978-3-031-36709-0_14
- インタプリタのプロトタイプ実装をした.
- Sano, J., Yamamoto, N., Ueda, K.:
Introducing Linear Implication Types to $\lambda_{GT}$ for Computing With Incomplete Graphs.
arXiv:2510.17429 (2025), プレプリント.
- パターンマッチングの型付けが綺麗にできるように型システムを拡張した.
-
「新しい言語を作ってしまう」研究は, あまり見かけない気がする. ゼロベースで新しい話をすることになるので既存研究との対応が分かりづらく, そもそも研究として評価しづらかったり(?), 既存言語でのソフトウェア資産の活用が難しくなるなど, 実用的な意味でも厳しさがあるからだと思う. なので私の研究テーマもそもそもの方向性として筋の良いものなのか, みたいな話はあるとは思う. この上なく面白いことをやっているとは勝手に思っている. ↩
-
分かりやすい説明ができないから短絡的にそう言っているだけで, あんまり本気ではない. 「超える」ってなんだ?となる. というか,理想的には Rust の wrapper みたいな形で提供したい. 「raw pointer を操作する unsafe コードを吐くが,安全性は $\lambda_{GT}$ 側で検証済み」みたいな. とはいえまだあまりに壁が高い. ↩